Lesson 6: Solid Waste Collection 

---

Analysis of Hauled Container Systems 

---

Variable definitions

• H = length of work day
• w = off-route factor
• h = haul time (1-way or round trip)
• t₁= time spent driving from dispatch site at beginning of day
• t₂= time spent driving to the dispatch site at the end of day
• N = # of trips made per day (same as # of locations serviced)
• L = # of locations or serviced in the work day
• C_n = # of containers per location
• dbc = time to drive between containers
• dbl = time to drive between locations
• s = time spent at disposal site
• pc = time to pick-up container
• uc = time to unload container
• zc = extra container manipulation time required for swap container operations
• P_HCS = container handling time at generation site (plus drive to next generation site for conventional system), used to simplify overall time equation
• T_HCS = time per round trip (to/from landfill), used to simplify the overall time equation

How can h, dbc, & dbl be estimated?

 ***** An integer number of locations must be serviced every day *****

Note: if 10 locations must be serviced but, only 5 containers/day possible then 2 vehicles or 2 days required to service the locations

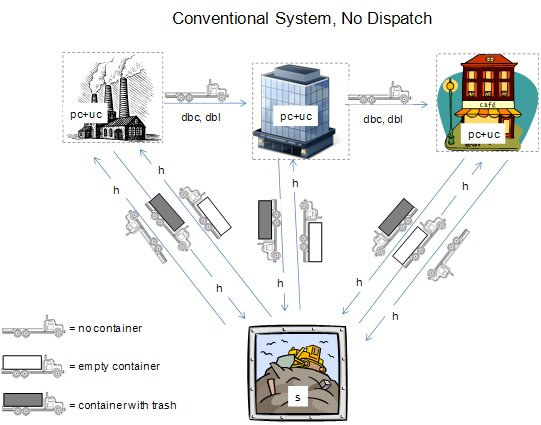
        Conventional - the system described in the text.  A round trip starting from the time the truck arrives at a waste generation site would be:

1. pickup the container, pc
2. drive to the disposal site with the used container, h
3. empty the container at the disposal site, s
4. drive to the generation site with the empty container, h
5. return the empty container to the pickup location in Step 1, uc
6. drive to the next pickup location with an empty truck (no container), dbc

Note that in order to include all of the collection activities in the round trip, the starting and stopping points are different.

        Swap container - this system is not described in the text.  The service vehicle arrives at a service location with an empty container.  It replaces the used container with the empty one and then hauls the used one to the disposal site.  A round trip starting from the time the truck leaves the disposal site would be:

1. drive to the pickup location with an empty container on the truck, h
2. unload the empty container, pickup the used container, reposition the empty container, (uc+pc+zc)
3. drive to the disposal site, h
4. empty the container at the disposal site, s
   The round trip sequence is now complete.  After the at-site time, the vehicle will start the round trip sequence again and drive to the next site.

Think:  Consider all of the activities for both the conventional and the swap HCS systems.  Which system would be more efficient time wise?  Can you think of any aesthetic concerns with either system?

An inherent assumption to these equations is that off-route time occurrs during all collection activites.

Consider the following figure and consider how you would write a general equation to determine:

(1) how many sites could be serviced in a work day or

(2) how long the work day would have to be to service a certain number of containers.

Answers are provided after the graphics.

for the service of three sites with one container at each site:

H(1-W) =3(pc+uc) + 3(s) + 8(h) + 2(dbl) = 3(pc+uc+s+2h+dbl) + 2h - dbl

then

H(1-W) = N_d(pc+uc+dbl+s+2h) + 2h - dbl

or

let P_HCS = pc+uc+dbl

H(1-W) = N_d(P_HCS+s+2h) + 2h - dbl

for the service of three sites with one container at each site:

H(1-W) =3(pc+uc+zc) + 3(s) + 6(h) = 3(pc+uc+zc+s+2h)

then

H(1-W) = N_d(pc+uc+zc+s+2h)

or

let P_HCS = pc+uc+zc

H(1-W) = N_d(P_HCS+s+2h)

Think: How would you adjust the above equations if it was determined that off-route activities only occured during hauling times, drive between containers/locations, and at the disposal site?

Think: Collection vehicles are often dispatched from a fleet maintenance site that is separate from the disposal site.  Consider the figures above (conventional and swap), add a dispatch site, and develop the time analysis equation.  Time spent driving from and to the dispatch site are t₁ and t₂ , respectively.