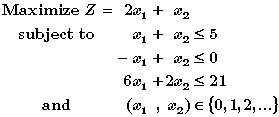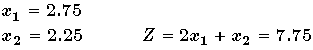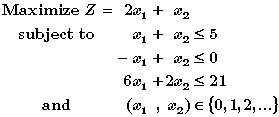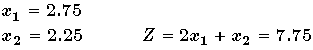To demonstrate the MIP algorithm, consider the following
integer programming problem.
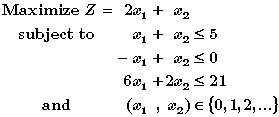
|
 |
|
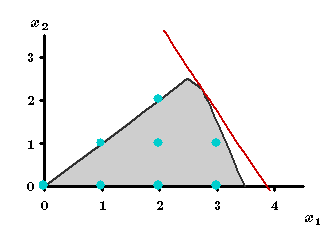
The optimal solution for the LP-relaxation, determined graphically, is: |
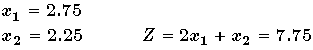 |
| Since the optimal solution for the LP-relaxation has noninteger values
for integer-restricted variables, it is not a feasible solution for the
original integer programming problem.
|
| If the optimal solution did have integer values for every integer-restricted
variable, then the optimal solution for the LP-relaxation would also be
the optimal solution for the original integer programming problem, and
the algorithm would be finished. |