Lesson 6: Solid Waste Collection 

---

Analysis of Stationary Container Systems 

---

>>>> Check out: The Winners of Beautiful Beasts at Waste Age

---

>>>> Check out: The Classic Refuse Trucks Web Page

>>>> Check out: Automated Container Loading System

   (What does this guy do for fun when he is not on winter break?)

>>>> Who is a Dustman's best friend? Classic Refuse Trucks at YouTube

---

Variable definitions

• H = length of work day
• W = off-route factor
• h = haul time (1-way or round trip)
• t₁= time spent driving from dispatch site at beginning of day
• t₂= time spent driving to the dispatch site at the end of day
• s = time spent at disposal site
• N = # of trips made per day
• v = volume of collection vehicle
• r = vehicle compaction factor
• c = container volume
• f = average container utilization factor
• C_n = average # of containers per location
• C_t = # of containers serviced in a trip
• C_t(max) = maximum number of containers the vehicle can hold - a function of truck capacity, compaction, and the volume of waste per container = (v*r)/(c*f)
• L = # of locations or serviced in the work day
• L_t =  # of locations serviced in a trip
• L_t(max) = maximum number of locations servicable in a trip - a function of truck capacity, compaction, and the volume of waste per location = C_max /C_n
• P_SCS = time spent servicing containers each trip.
  • Time spent loading and replacing containers and driving between locations
  • Function of the # of sites serviced during the trip and the # of containers at each location (an average value is used)
  • Equations for calculating:
    • The following two equations are typically used when 'dbl' is large (ie - commercial container systems or rural areas)
      • P_SCS = C_t*(uc) + (L_t - 1)*(dbl)
      • P_SCS(max) = C_t(max)*(uc) + (L_t(max) - 1)*(dbl)
        • uc = average time required to service one stationary container, min/container
    • The next two equations are typically used when 'dbl' is small (ie - residential container systems or dense urban areas)
      • P_SCS = L_t*{dbl +k₁C_n + k₂*(PRH)}
      • P_SCS(max) = L_t(max)*{dbl +k₁C_n + k₂*(PRH)}
        • dbl = average drive between location time, min/location (typical value: ~0.72 min/location)
        • k₁ = constant related to the service time per container, min/container (typical value: ~0.18 min/container)
        • k₂ = constant related to the time required to collect waste from the back of a residence, min/loc/PRH (typical value: ~? min/location/PRH)
        • PRH = residences requiring back of house service, percent

***** An integer number of locations must be serviced every day *****

Note: if 10 trips must be made per day but, only 5 trips/day possible then 2 vehicles or 2 days required to service the locations 

Types of Service Areas

Estimating h, dbc, & dbl:

Review the "Estimating Haul Time" PDF file available on the WebCT course web-site under Online Lessons.

1. the amount of waste collected by a packer truck each trip and
2. the time available for completing the collection tasks

The difference between the analysis of an HCS and and SCS is that in an HCS, the collection vehicle hauls one container at a time to and from the disposal site while in an SCS the collection vehicle (usually a packer truck) collects waste from as many containers as possible prior to hauling the waste to the disposal site. The pickup time per trip (P_SCS) is then a function of the number of containers serviced on each trip and the time spent servicing each container.   

Vehicle Capacity Analysis (Volumetric)
Based on how much trash the vehicle can hold and how much waste the average site generates, the maximum number of sites servicable by the vehicle is calculated.

Variable Definitions

• C_t, number of containers serviced per trip
  • C_t(max) maximum number of containers the vehicle can hold
  • C_t(max) = (v*r)/(c*f) = (effective vehicle volume)/(volume of waste in a container)
• C_n, average number of containers at generation sites
• L_t, number of locations serviced per trip = C_t/C_n
  • L_t(max) = C_t(max)/Cn
  • Note: When an non-integer value for L_t(max) is calculated, it is rounded down since rounding up would result in an overly full vehicle.
• N, number of trips per day
  • Estimate of N_t = V_d/(v*r) = waste volume to be collected/effective vehicle volume.
• v = vehicle volume
• r = vehicle compaction factor
• c = container volume
• f = container utilization factor, reflects how full container is.
• V_{d or w} = volume of waste to be collected per day or week, respectively

Time Analysis

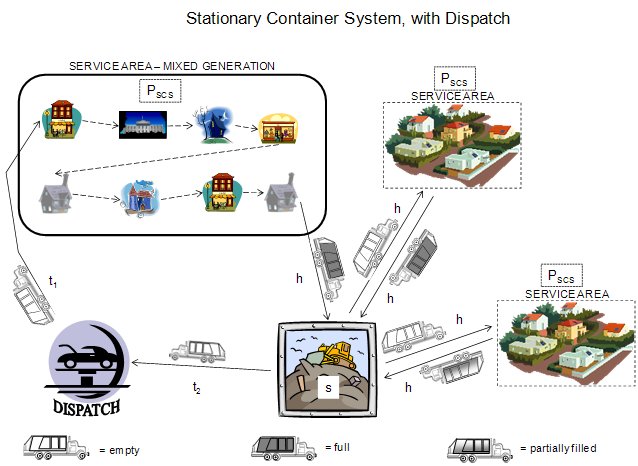
Two types of trips may be made during the course of a day:

1. Complete trip fills the vehicle to capacity
2. Partial trips only have time to fill a fraction of the vehicle,

Overall Time Equations for Dispatch Scenario:
An inherent assumption to the equations below is that off-route time occurrs during all collection activites.

Primary:         H(1-W) = t₁ + t₂ + N*(P_SCS(max)  + s + 2h) - h
Secondary:     H(1-W) = t₁ + t₂ + N'*(P_SCS(max) + s + 2h) + h + s + P'_SCS

There is still only so much time availabe in a day to complete all of the tasks required for waste collection and disposal.  When a time analysis is conducted to determine the number of locations which can be serviced by one packer truck in a day, the following steps are used:

1. The maximum number of containers and locations servicable per trip is calculated using the effective volume of the truck and the amount of waste per container or site.
2. P_SCS is calculated.
3. The number of trips possible per day (N) is solved for using the primary overall time equation.
4. If N is an integer then the number of location is serviced is equal to N*L_t(max). If N is not an integer then, goto Step 5.
5. When N is a non-integer, the trips done must be divided into complete and partial trips as defined above.
   1. Set N' equal to the integer portion of N calculated in Step 3.  Rounding N down to an integer value (N') gives the number of complete trips which can be done.
   2. The fractional portion of N represents the time available to do a partial trip. To determine how many locations can be serviced in this partial trip (L_t'), all of the tasks involved in the full tripsmust be deducted from the workday, then the remaining time must be analyzed to determine how much trash could be collected.
   3. Solve the secondary overall time equation for P'_SCS.
   4. Solve the equation for P'_SCS for L_t.  Let this L_t = L_t'
   5. The number of locations serviced then equals N'*L_t(max) + L_t'

• How would the time span of week be analyzed?
• How would curbside recycling programs be analyzed (volumetric and time)? 
• How does this relate to an economic analysis (capital costs, labor costs)?