Material Studies with Microwaves
Traditional Microwave Studies of Electrodynamics in Materials
Traditional microwave studies use the perturbation that a sample introduces to a microwave resonator to study the electrodynamics in materials. By measuring the transmitted signal (two-port) or the reflected signal (one-port) from a microwave resonator, one can fully address the electromagnetic (EM) characteristics of the resonator, including its resonant frequencies, f0’s, losses (through quality factor measurements), couplings (through phase-sensitive or S-parameter measurements), etc. When a resonator is coupled to a sample, above characteristics of the resonator will be slightly changed. This is because the resonator is no longer the same but includes the coupled sample. Typically a sample is placed inside a resonant cavity or on top of a strip-line resonator and coupled to the resonator by immersing in uniform fields of the resonator. The extraction of EM properties of materials is made possible by the well established cavity perturbation theory.[1-2] By comparing the perturbed (with samples) characteristics with the unperturbed (no sample) ones, it allows one to address electromagnetic properties, e.g. surface impedance, complex conductivity, and so on.
Scanning Near-field Microwave Microscopy (SNMM)
However, the spatial resolution of the traditional microwave methods is limited by the wavelengths of microwaves, typically on the length scales of cm or larger, hence only good for studies of bulk material properties. To overcome this limitation in far-field measurements and enable studies of local microwave properties of materials, experimental methods with near-field microwaves have been developed and the applications have been expanded over the years.
The earliest work of near-field microwave measurements was done by Frait [3-4] and Soohoo [5] who used resonators with small apertures to couple to samples and scan for local properties of interests. The near-field coupling does not suffer from the resolution limit set by the free-space wavelengths, and can achieve sub-mm resolution which is determined by the coupling geometries. Similar microwave analysis is carried out as in the traditional measurements, but in this scenario, the perturbation is induced by a very small portion of a sample which couples to the microwave system through the near-field. Various forms of near-field microwave microscopy were developed for frequencies ranging from optical to microwaves using optical fibers, waveguides, microstrip resonators, coaxial cables, and so on.[6-28] I have first-hand experience with several novel forms of Scanning Near-field Microwave Microscopes (SNMM) through the work in Anlage’s group in UMD,[29-37] and pursue opportunities for developing a similar instrumentation in Mercer.
Microwave Properties of Superconductors
Non-linear Microwave Properties of Superconductors
Nonlinear properties of superconductors have drawn both industrial and academic interests in the past decades since the discovery of high-temperature superconductors (HTSC). Considering microwave devices made of HTSC, higher order harmonics and/or inter-modulation distortions (IMD) arise due to the nonlinear properties of the superconductors, and consequently limit the applications of HTSC to low microwave power applications. Great industrial efforts had been made to reduce the nonlinear behaviors significantly through improving the quality of the HTSC films and eliminating/minimizing the structural defects. However, nonlinearities in superconductors can not be completely eliminated because superconductivity is intrinsically nonlinear, as described by the nonlinear Meissner effect. The following discusses this phenomenon in greater details.
The nonlinear Meissner effect is a phenomenon expected in all superconductors. When a superconducting current flows in a superconductor, the current also breaks Cooper pairs and enhances quasi-particle excitations. The consequence of this effect is the reduction of the super-fluid density and the magnetic screening effectiveness, which leads to a supercurrent-dependent super-fluid density or magnetic penetration depth, predicted by both the BCS[38-40] and Ginzburg-Landau theories.[41] Fig. 1 shows the nonlinear responses from a superconductor measured as a function of temperature near Tc. Dramatic enhancement is observed near Tc due to the very weak superconductivity which is most accessible to the pair-breaking effect of supercurrents.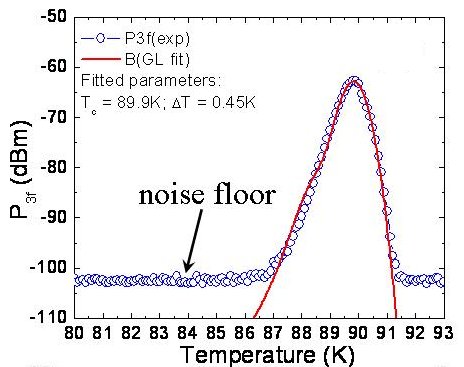
Fig. 1 Third harmonic responses from a YBCO thin film near Tc.
It should also be noted that the nonlinear Meissner effect is merely responsible for the nonlinear responses from superconductors due to the intrinsic superconductivity, and is normally very weak and only becomes dominant and observable near Tc (for all superconductors) or at low temperature limits (for d-wave superconductors). When other sources of nonlinearity are present, such as structural defects (boundaries, edges, cracks, etc.) and impurities, they dominate the nonlinear responses for the majority of the temperature range. Fig. 2(a) & (b) demonstrate the local nonlinear responses measured at second and third harmonics on YBCO bi-crystal boundaries (Tc = 89 K) at T = 60 K. At this temperature, the nonlinear Meissner effect is not observable and the nonlinear responses are solely dominated by the structural defects, the bi-crystal boundary in this case. While the majority of the film shows no signs of nonlinear responses, tremendously enhancements are observed near the boundary. The width of the feature (~ 0.5 mm) shown in the images is determined by the spatial resolution of the scanning probe available then.[36-37] Fig. 2
Second and third harmonic images on a YBCO bi-crystal grain boundary. The enhanced responses in the middle of the images mark the approximate location of the grain boundary.
Magnetic Imaging
Local Magnetic Resonance Phenomena
The rapidly increasing read/write speed and density of the magnetic storage media has led to an increasing interest in local microwave magnetic properties of materials, the homogeneity of Curie temperatures, local magnetizations, and phase separation into magnetic/non-magnetic domains. While scanning microscopes have been designed to image radio frequency magnetic fields,[42-44] electron paramagnetic resonances (EPR),[45] and ferromagnetic resonances (FMR),[3,46-48] very few of these techniques measure magnetic properties on sub-mm length scales.[49-50] Our studies of local magnetic properties using the SNMM developed in UMD was one of the pioneering works to measure local magnetic permeability and FMR fields with the spatial resolution of ~ 0.5 mm.[31] As shown in Fig. 3(a) & (b), the SNMM is able to distinguish between the metallic glasses with the same electric resistivity (r = 150 mWcm) and very similar geometries, but substantially different magnetic properties (paramagnetic vs. ferromagnetic). This result demonstrates the unique ability of the SNMM in measuring local variations of permeability. 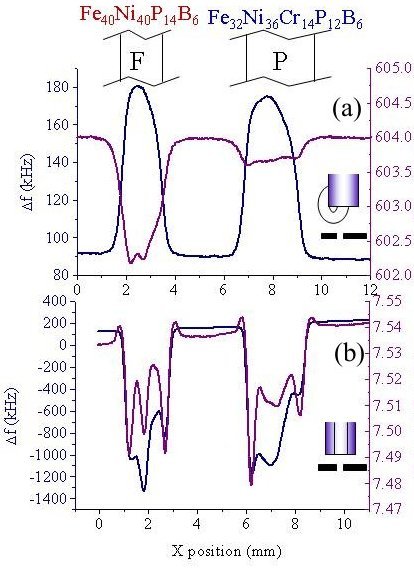
Fig. 3
Line-scans of Df and Q accross ferromagnetic and paramagnetic metallic glasses tapes with the (a) the magnetic and (b) the electric sensing probe. Constrast in magnetic properties is observed in the magnetic sensing probe, but not in the electric one.I also used the same SNMM to study the local FMR in a colossal magnetoresistive (CMR) material, La0.8Sr0.2MnO3 (LSMO) with Curie temperature TC = 305.5 K. The magnetic dipoles in the material undergo precessions in an external dc magnetic field. If an ac magnetic field is applied at just the frequency of the precession frequency in a given dc field, the energy of the ac magnetic field will be absorbed, exhibiting a phenomenon generally called "magnetic resonance". However, due to the inevitable variation of local magnetization in any given sample, the external magnetic field experienced by each magnetic dipole is different. In another word, if an ac magnetic field is applied at a fixed frequency, the corresponding dc magnetic field for "magnetic resonance" to occur will vary over a sample. By applying microwaves at a fixed frequency to an LSMO crystal at T = 301.5 K, the local FMR field is imaged as shown in Fig. 4(a) & (b). Details of these studies are found in Ref.[31]. Fig. 4
Variations of Df and Q in a CMR crystal indicating the variation of FMR fields in the crystal.
References
[1] J. C. Slater, "Microwave Electronics," Rev. Mod. Phys. 18,
441-521 (1946); L. C. Maier, Jr. and J. C. Slater, "Field Strength
Measurements in Resonant Cavities," J. Appl. Phys. 23, 68-83 (1952).
[2] O. Klein, S. Donovan, M. Dressel, and G. Grüner, "Microwave Cavity
Perturbation Technique: Part I: Principles," Int. J. Infrared and
Millimeter Waves 14, 2423-2457 (1993); S. Donovan, O. Klein, M. Dressel,
K. Holczer, and G. Grüner, "Microwave Cavity Perturbation Technique:
Part II: Experimental Scheme," Int. J. Infrared and Millimeter Waves 14,
2459-2487 (1993); M. Dressel, O. Klein, S. Donovan, and G. Grüner,
"Microwave Cavity Perturbation Technique: Part III: Applications," Int.
J. Infrared and Millimeter Waves 14, 2489-2517 (1993).
[3] Zdenek Frait, "The use of high frequency modulation in studying
ferromagnetic resonance," Czeck. J. Phys. 9, 403-404 (1959)
[4] Z. Frait, V. Kambersky, Z. Malek, and M. Ondris, "Local variations
of uniaxial anisotropy in thin films," Czeck. J. Phys. B10,
616-617 (1960).
[5] R. F. Soohoo, "A Microwave Magnetic Microscope," J. Appl. Phys.
33, 1276-1277 (1962).
[6] C. A. Bryant and J. B. Gunn, "Noncontact Technique of the Local
Measurement of Semiconductor Resistivity," Rev. Sci. Instrum. 36,
1614-1617 (1965).
[7] Bosisio, Giroux, and Couderc, "Paper Sheet Moisture Measurements by
Microwave Phase Perturbation Techniques," J. Microwave Power 5, 25-34
(1970).
[8] Tanabe and Joines, "A Nondestructive Method for Measuring the
Complex Permittivity of Dielectric Materials at Microwave Frequencies
Using an Open Transmission Line Resonator," IEEE Trans. Instrum. and
Meas. IM-25, 222-226 (1976).
[9] M. A. Stuchly and S. S. Stuchly, "Coaxial Line Reflection Methods
for Measuring Dielectric Properties of Biological Substances at Radio
and Microwave Frequencies - A Review," IEEE Trans. Instrum. and Meas.
IM-29, 176-183 (1980); M. A. Stuchly, M. M. Brady, S. S. Stuchly and G.
Gajda, "Equivalent Circuit of an Open-Ended Coaxial Line in a Lossy
Dielectric," IEEE Trans. Instrum. and Meas. IM-31, 116-119 (1982); T. W.
Athey, M. A. Stuchly and S. S. Stuchly, "Measurement of Radio Frequency
Permittivity of Biological Tissues with an Open-Ended Coaxial Line: Part
I," IEEE Trans. Microwave Theory and Tech. MTT-30, 82-86 (1982); M. A.
Stuchly, T. W. Athey, G. M. Samaras and G. E. Taylor, "Measurement of
Radio Frequency Permittivity of Biological Tissues with an Open-Ended
Coaxial Line: Part II - Experimental Results," IEEE Trans. Microwave
Theory and Tech. MTT-30, 87-92 (1982); G. B. Gajda and S. S. Stuchly,
"Numerical Analysis of Open-Ended Coaxial Lines," IEEE Trans. Microwave
Theory and Tech. MTT-31, 380-384 (1983).
[10] R. J. Gutman and J. M. Borrego, "Microwave scanning microscopy for
planar structure diagnostics," IEEE MTT Digest, 281-284 (1987);
Bhimnathwala and J. M. Borrego, "Measurement of the sheet resistance of
doped layers in semiconductors by microwave reflection," J. Vac. Sci.
Technol. B 12 , 395-398 (1994).
[11] G. R. Eaton, and S. S. Eaton, "EPR Imaging: Progress and
Prospects," Bull. Magn. Resonance 10, 22-31 (1987).
[12] M. Fee, S. Chu and T. W. Hänsch, "Scanning electromagnetic
transmission line microscope with sub-wavelength resolution," Optics
Communications 69, 219-224 (1989).
[13] R. Merz, F. Keilmann, R. J. Haug, and K. Ploog, "Nonequilibrium
Edge-State Transport Resolved by Far-Infrared Microscopy," Phys. Rev.
Lett. 70, 651-653 (1993); F. Keilmann, "FIR Microscopy," Infrared Phys.
Technol. 36, 217-224 (1995); F. Keilmann, D. W. van der Weide, T.
Eickelkamp, R. Merz, and D. Stöckle, "Extreme sub-wavlength resolution
with a scanning radio-frequency transmission microscope," Optics Commun.
129, 15-18 (1996); B. Knoll, F. Keilmann, A. Kramer, and R. Guckenberger,
"Contrast of microwave near-field microscopy," Appl. Phys. Lett. 70,
2667-2669 (1997).
[14] M. Tabib-Azar, N. Shoemaker and S. Harris, "Non-destructive
characterization of materials by evanescent microwaves," Meas. Sci.
Tech., 4, 583-590 (1993); M. Tabib-Azar, D. -P. Su, A. Pohar, S. R.
LeClair, and G. Ponchak, "0.4 µm spatial resolution with 1 GHz ( = 30
cm) evanescent microwave probe," Rev. Sci. Instrum., 70, 1725-1729
(1999); M. Tabib-Azar, P. S. Pathak, G. Ponchak, and S. LeClair,
"Nondestructive superresolution imaging of defects and nonuniformities
in metals, semiconductors, dielectrics, composites, and plants using
evanescent microwaves," Rev. Sci. Instrum., 70, 2783-2792 (1999); M.
Tabib-Azar, R. Ciocan, G. Ponchak, and S. R. LeClair, "Transient
thermography using evanescent microwave microscope," Rev. Sci. Instrum.,
70, 3387-3390 (1999); G. Ponchak, D. Akinwande, R. Ciocan, S. R. LeClair
and M. Tabib-Azar, "Evanescent Microwave Probes Using Coplanar Waveguide
and Stripline for Super-Resolution Imaging of Materials," IEEE MTT-S
Digest, (1999).
[15] S. J. Stranick and P. S. Weiss, "A versatile
microwave-frequency-compatible scanning tunneling microscope," Rev. Sci.
Instrum. 64, 1232-1234 (1993); S. J. Stranick and P. S. Weiss, "A
tunable microwave frequency alternating current scanning tunneling
microscope," Rev. Sci. Instrum. 65, 918-921 (1994); L. A. Bumm and P. S.
Weiss, "Small cavity nonresonant tunable microwave-frequency alternating
current scanning tunneling microscope," Rev. Sci. Instrum. 66, 4140-4145
(1995).
[16] G. Q. Jiang, W. H. Wong, E. Y. Raskovich, W. G. Clark, W. A. Hines,
J. Sanny, "Open- ended coaxial-line technique for the measurement of the
microwave dielectric constant for low-loss solids and liquids," Rev. Sci.
Instrum. 64, 1614-1621 (1993).
[17] K. Asami, "The scanning dielectric microscope," Meas. Sci. Technol.
5, 589-592 (1994).
[18] Y. Manassen, "Scanning Probe Microscopy and Magnetic Resonance,"
Adv. Mater. 6, 401-404 (1994).
[19] Y. Cho, A. Kirihara and T. Saeki, "Scanning nonlinear dielectric
microscope," Rev. Sci. Instrum. 67, 2297 (1996).
[20] M. Golosovsky and D. Davidov, "Novel millimeter-wave near-field
resistivity microscope," Appl. Phys. Lett. 68, 1579-1581 (1996); M.
Golosovsky, A. Galkin, and D. Davidov, "High-Spatial Resolution
Resistivity Mapping of Large-Area YBCO Films by a Near-Field
Millimeter-Wave Microscope," IEEE MTT 44, 1390-1392 (1996); M.
Golosovsky, A. Lann, and D. Davidov, "A millimeter-wave near-field
scanning probe with an optical distance control," Ultramicroscopy 71,
133-141 (1998).
[21] Y. Lu, T. Wei, F. Duewer, Y. Lu, N. Ming, P. G. Schultz and X.-D.
Xiang, "Nondestructive Imaging of Dielectric-Constant Profiles and
Ferroelectric Domains with a Scanning-Tip Microwave Near-Field
Microscope," Science 276, 2004-2006 (1997); C. Gao, and X.-D. Xiang,
"Quantitative microwave near-field microscopy of dielectric properties,"
Rev. Sci. Instrum. 69, 3846-3851 (1998).
[22] Z. Zhang, P. C. Hammel and P. Wigen, "Observation of ferromagnetic
resonance in a microscopic sample using magnetic resonance force
microscopy," Appl. Phys. Lett. 68, 2005-2007 (1996); Z. Zhang, P. C.
Hammel, M. Midzor, M. L. Roukes, and J. R. Childress, "Ferromagnetic
resonance force microscopy on microscopic cobalt single layer films,"
Appl. Phys. Lett. 73, 2036-2038 (1998).
[23] M. J. Werner and R. J. King, MRS Proc. (1996).
[24] John Gallop, L. Hao, F. Abbas, "Spatially Resolved Measurements of
HTS Microwave Surface Impedance, "Physica C 282-287, 1579-1580 (1997);
L. Hao, J. C. Gallop, "Spatially Resolved Measurements of HTS Microwave
Surface Impedance," IEEE Trans. Appl. Supercond. 9, 1944-1947 (1999).
[25] J. Bae, T. Okamoto, T. Fujii, K. Mizuno, T. Nozokido, "Experimental
demonstration for scanning near-field optical microscopy using a metal
micro-slit probe at millimeter wavelengths," Appl. Phys. Lett. 71,
3581-3583 (1997).
[26] N. Qaddoumi and R. Zoughi, "Preliminary study of the influences of
effective dielectric constant and nonuniform probe aperture field
distribution on near field microwave images," Materials Evaluation,
Oct., 1169-1173 (1997).
[27] U. Durig, D. W. Pohl and F. Rohmer, "Near-field optical-scanning
microscopy," J. Appl. Phys. 59, 3318-3327 (1986).
[28] F. Keilmann, D. W. van der Weide, T. Eickelkamp, R. Merz, and D.
Stöckle, "Extreme sub-wavlength resolution with a scanning
radio-frequency transmission microscope," Optics Commun. 129, 15-18
(1996).
[29] C. P. Vlahacos, R. C. Black, S. M. Anlage, A. Amar, and F. C.
Wellstood, “Near-field Scanning Microwave Microscope with 100 m
Resolution,” Appl. Phys. Lett. 69, 3272-3274 (1996).
[30] D. E. Steinhauer, C. P. Vlahacos, S. K. Dutta, B. J. Feenstra, F.
C. Wellstood, and Steven M. Anlage, “Quantitative Imaging of Sheet
Resistance with a Scanning Near-Field Microwave Microscope,” Appl. Phys.
Lett. 72, 861-863 (1998).
[31] S.C. Lee, C. P. Vlahacos, B. J. Feenstra, Andrew Schwartz, D. E.
Steinhauer, F. C. Wellstood, and Steven M. Anlage, “Magnetic
Permeability Imaging of Metals with a Scanning Near-Field Microwave
Microscope”, Appl. Phys. Lett. 77, 4004 (2000).
[32] Dragos I. Mircea, Sheng-Chiang Lee, Matthew C. Sullivan, Steven M.
Anlage, Benjamin S. Palmer, B. Maiorov, and E. Osquiguil, “Evidence for
Fluctuation-induced Resistive Microwave Nonlinearities above Tc in
Underdoped Cuprates”, submitted to Phys. Rev. B (2006).
[33] Sheng-Chiang Lee, Mathew Sullivan, Gregory R. Ruchti, Steven M.
Anlage, Benjamin Palmer, B. Mariorov, E. Osquiguil, “Doping-Dependent
Nonlinear Meissner Effect and Spontaneous Currents in High-Tc
Superconductors”, Phys. Rev. B 71, 014507 (2005); cond-mat/0405595.
[34] Sheng-Chiang Lee and Steven M. Anlage, “Doping Dependent
Time-Reversal Symmetric Nonlinearity of YBa2Cu3O7-d thin films”, Physica
C 408-410, 324 (2004); cond-mat/0306416v2.
[35] Sheng-Chiang Lee and Steven M. Anlage, “Study of Local Nonlinear
Properties Using a Near-Field Microwave Microscope”, IEEE Trans. Appl.
Supercond., vol. 13, pp.3594-3597 (2003).
[36] Sheng-Chiang Lee, Su-Young Lee, and Steven M. Anlage, “Microwave
Nonlinearities of an Isolated Long YBa2Cu3O7-d Bi-crystal Grain
Boundary”, Phys. Rev. B 72, 024527 (2005); cond-mat/0408170.
[37] Sheng-Chiang Lee and Steven M. Anlage, “Spatially-Resolved
Nonlinearity Measurements of YBa2Cu3O7-d Bi-Crystal Grain Boundaries”, Appl. Phys. Lett. 82, 1893 (2003).
[38] S. K. Yip and J. A. Sauls, “Nonlinear Meissner Effect in CuO
Superconductors,” Phys. Rev. Lett. 69, 2264 (1992).
[39] D. Xu, S. K. Yip, and J. A. Sauls, “Nonlinear Meissner Effect in
Unconventional Superconductors,” Phys. Rev. B 51, 16233 (1995).
[40] T. Dahm and D. J. Scalapino, “Theory of Intermodulation in a
Superconducting Microstrip Resonator,” J. Appl. Phys. 81, 2002 (1997).
[41] J. Gittleman, B. Rosenblum, T. E. Seidel, and A. W. Wicklund,
“Nonlinear Reactance of Superconducting Films,” Phys. Rev. 137, A527
(1965).
[42] R. C. Black, F. C. Wellstood, E. Datsker, A. H. Miklich, D. T.
Nemeth, D. Koelle, F. Ludwig, and J. Clarke, “Microwave microscopy using
a superconducting quantum interference device,” Appl. Phys. Lett. 66,
99-101 (1995).
[43] Y. Gao and I. Wolff, “A New Miniature Magnetic Field Probe for
Measuring Three-Dimensisonal Fields in Planar High-Frequency Circuits,”
IEEE Trans. Microwave Theory Tech. 44, 911-918 (1996).
[44] V. Agrawal, P. Neuzil, and D. W. van der Weide, “A Microfabricated
Tip for Simultaneous Acquisition of Sample Topography and High-Frequency
Magnetic Field,”
[45] M. Ikeya and T. Miki, "ESR Microscopic Imaging with Microfabricated
Field Gradient Coils," Jap. J. Appl. Phys. 26, L929-L931 (1987); M.
Ikeya, M. Furusawa, and M. Kasuyai, "Near-field scanning electron spin
resonance microscopy," Scanning Microscopy 4, 245-248 (1990).
[46] Z. Zhang, P. C. Hammel, M. Midzor, M. L. Roukes, and J. R.
Childress, “Ferromagnetic resonance force microscopy on microscopic
cobalt single layer films,” Appl. Phys. Lett. 73, 2036-2038 (1998).
[47] K. Wago, D. Botkin, C. S. Yannoni, and D. Rugar, “Paramagnetic and
ferromagnetic resonance imaging with a tip-on-cantilever magnetic
resonance force microscope,” Appl. Phys. Lett. 72, 2757-2759 (1998).
[48] S. E. Lofland, S. M. Bhagat, H. L. Ju, G. C. Xiong, T. Venkatesan,
and R. L. Greene, “Ferromagnetic resonance and magnetic homogeneity in a
giant-magnetoresistance material La2/3Ba1/3MnO3,” Phys. Rev. B 52,
15058-15061 (1995).
[49] Y. Martin and H. K. Wickramasinghe, “Magnetic Imaging by “Force
Microscopy” with 1000Å Resolution,” Appl. Phys. Lett. 50, 1455-1457
(1987).
[50] S. Y. Yamamoto and S. Schultz, “Scanning Magnetoresistance
Microscopy,” Appl. Phys. Lett. 69, 3263-3265 (1996).