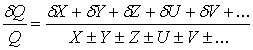
Listed are some of the most basic rules for uncertainty propagations in algebraic manipulations. There are two ways of expressing uncertainties: absolute uncertainties and fractional uncertainties (also known to you as "percent uncertainties"). These rules apply to simple uncertainty analysis as you use in most of your data analysis in PHY121L, PHY142L, and PHY162L. Note that these rules apply when these fractional uncertainties are much less than 1. The notations used for measurements, absolute uncertainties, and fractional uncertainties are explained below.
Upper case letters, e.g. X, Y, Z, etc., are used for measured quantities.
Lower case letters, e.g. a, b, c, etc., are used for constants.
"d" of a quantity represents the absolute uncertainty associated with this measurement, e.g.
dX, dY, dZ,
etc.
dX/X represents the fractional uncertainty of measured
quantity X.
The "percent uncertainty" used in the report guideline is simply expressing
dX/X in terms of percentage, i.e. (dX/X)
´ 100%.
You should also note that if your data require statistical analysis, then the propagations of statistical uncertainties (standard deviations) do not follow these rules (these rules set the upper-bound of the uncertainties), and shall be derived differently.
If the derived quantity Q comes through additions and/or subtractions among measured quantities, it is better to consider absolute uncertainties when we investigate the propagations of uncertainties. The fractional uncertainty can be found after obtaining the absolute uncertainty of the derived quantity.
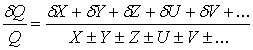 |
When the derived quantity Q is obtained through productions and divisions among measured quantities, it is more convenient to consider fractional uncertainties than absolute uncertainties.
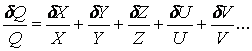 |
If the derived quantity Q is simply a measured quantity X multiplied by a constant, a, the fractional uncertainty of the derived quantity remains the same as of the measured quantity.
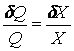 |
If the derived quantity Q is the measured quantity X to a constant power, a, then the fractional uncertainty of the derived quantity is "a" times of the fractional uncertainty of the measured quantity.
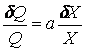 |